一、从一次需求说起

在做一个在线课件的项目，类似于 web 端在线的 ppt 制作工具。制作课件避免不了各种进入退出动画，ppt 有的，公司工具也必须有。各种淡入淡出，从上、下、左、右方向飞出飞入，css3 动画安排上！正在我写的不亦乐乎，觉得微软入场动画也不过如此的时候，产品经理来了。“ppt 有的动画咱们工具必须有，ppt 没有的动画，咱么也要有！我们要让老师自定义动画，制作课件的时候用鼠标画出路径，然后保存路径数据，播放的时候元素沿着路径飞进来。” 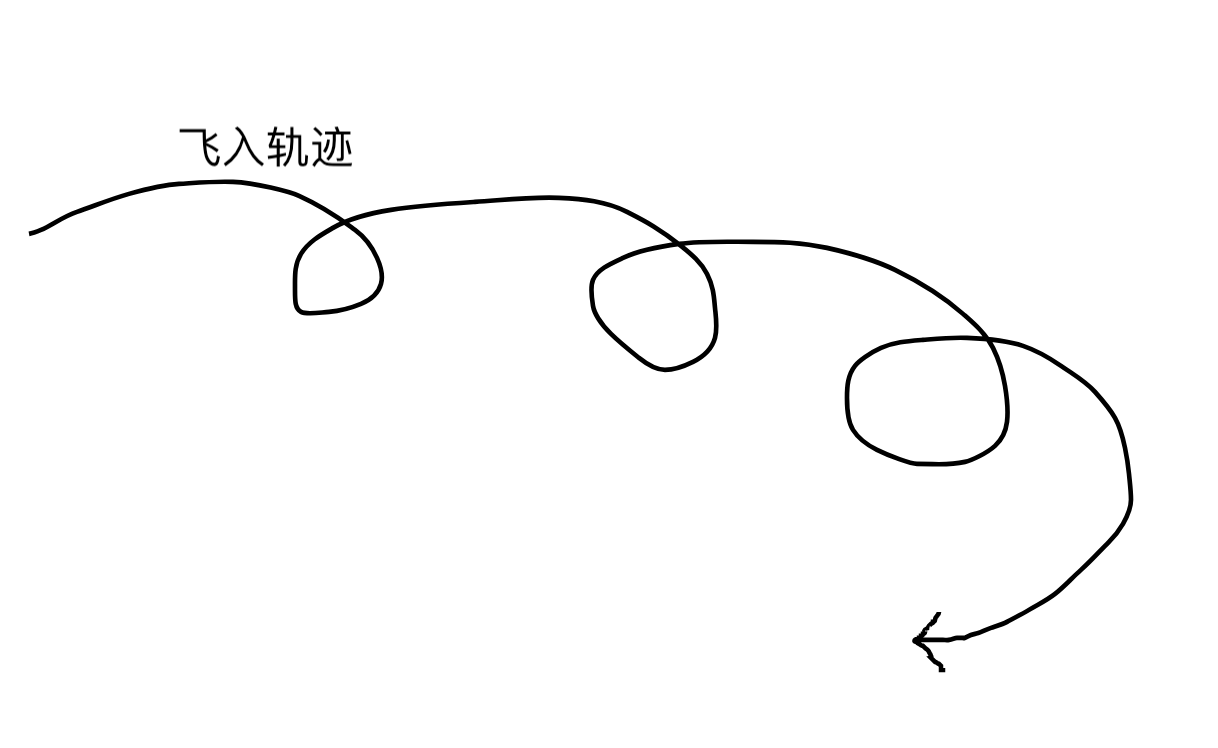在我意识到产品经理不是在开玩笑的时候，我断然拒绝了接需求。当产品经理带着老板又来提这个需求的时候，我感觉到事情没这么简单······

最终还是我妥协了，自认为我还是刚不过老板的。

这个需求，将我初中的知识用的淋漓尽致（感谢初中老师）。

二、解决技术难题

要记录鼠标轨迹，一定要用到鼠标的 mousemove 事件，mousemove 事件能获取一系列的鼠标位置点，就可以控制元素一个点一个点“蹦”过去。在我脑补了一个青蛙沿着一个一个黑点跳过去的画面后，我马上放弃了这个想法。 动画移动是平滑的，绝对不是离散的。开始搜“如何将一系列离散的位置点拟合成平滑的曲线？”移步博客记录鼠标轨迹, 生成 svg 路径。

路径数据有了，是三次贝塞尔曲线，剩下的就是构建 svg 路径，让元素动起来了。

如何让元素沿着 svg 曲线移动？

SVGPathElement接口对应于<path>元素。这个接口有两个很有用的方法**getTotalLength()和getPointAtLength()**，前者得到 path 路径全长，后者传入长度得到坐标。

有了这些知识就可以做很多事情了，知道总长和总时间就可以知道速度，知道速度也知道当前走过的时间就可以算出当前走过的路程，知道当前的路程就知道了当前在 path 上的坐标，知道了当前坐标就能让元素就位了！很简单的路程速度与时间的方程，s = vt。

撸代码

// 首先构建出path元素
const path =
  "M182,171 C183.25,171,185,171,187,171 C189,171,188.75,170.75,190,171 ......";
const pathEl = document.createElementNS("http://www.w3.org/2000/svg", "path");
pathEl.setAttribute("d", path);
// 记录总时长，总长度和起始时间
const duration = 2000; // ms
const totalLength = pathEl.getTotalLength(); // 总长
let curPosition = pathEl.getPointAtLength(0); // 当前坐标,一开始是在起始点
const startTime = new Date().getTime(); // 起始时间

requestAnimationFrame(step); // js动画必备方法
// 动画前进一小步
function step() {
  const nowTime = new Date().getTime();
  const t = (nowTime - startTime) / duration; // 时间进度 0~1
  const progress = totalLength * t; // 当前走过的路程
  curPosition = pathEl.getPointAtLength(progress); // 当前位置点的坐标
  $e.style.transform = `translate(${curPosition.x}px, ${curPosition.y}px)`;
  if (t <= 1) {
    requestAnimationFrame(step);
  }
}

看 demo

又一次需求

一个元素收起的动画，动点从不同的位置沿着不同的路径飞入同一个目标，就像这个样子。 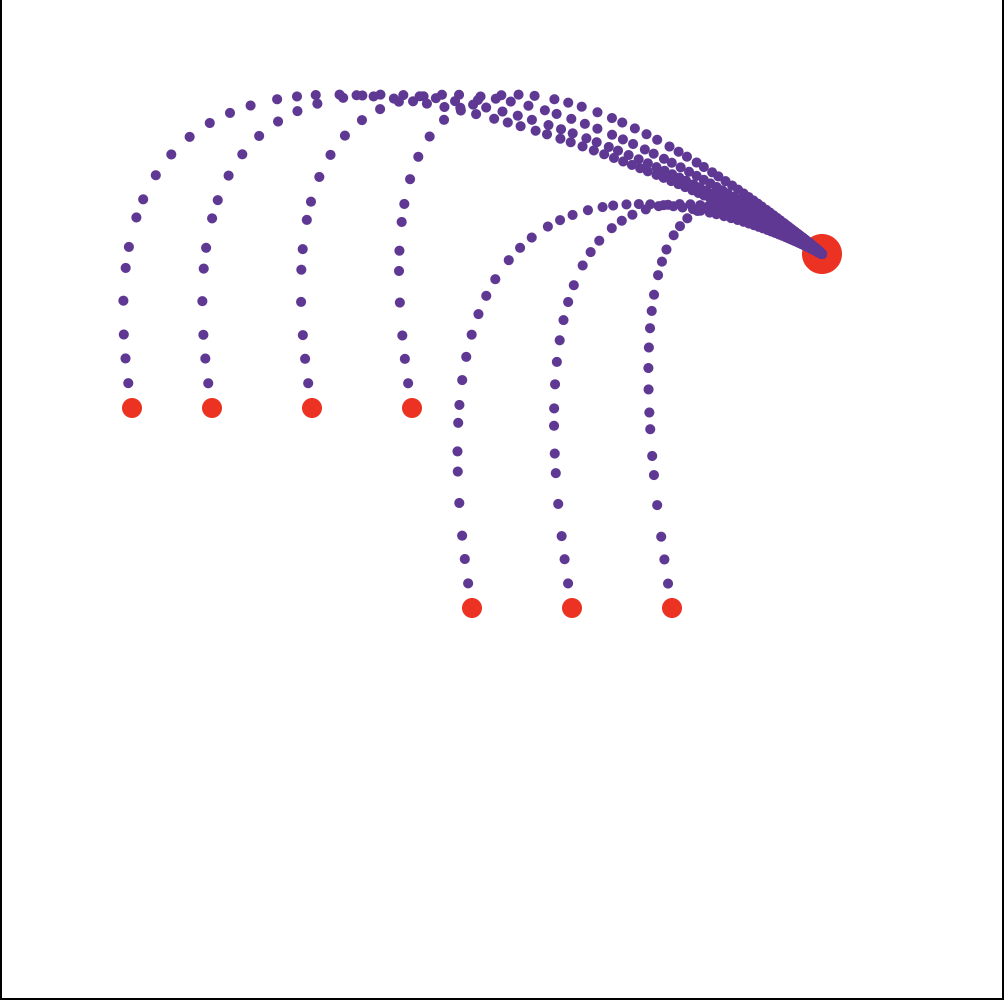有了上边的经验，实现起来就不慌了。 沿着上边的思路，先确定 svg 路径，再确定时间（动效老师直接给出），完全没问题！

确定路径

动效老师在了解到这是贝塞尔曲线后，马上给出了 24 个控制点的数据。因为起点一共有 12 个，终点有一个，这就有 12 条路径，每一条路径两个控制点，一共有 24 个控制点坐标。看着控制点坐标数据表格，我陷入了沉思，这咋维护？如果起点和终点的相对位置变了，岂不是需要重新计算 24 个控制点，这谁受得了？

理想情况是根据某种规律，由起点和终点的坐标计算出控制点坐标，起点和终点前端可以自己获取。经过观察，元素的移动路径是有规律的，起点在终点左边的点移动曲线向左弯曲，起点在终点右边的曲线向右弯曲，起点和终点的 x 坐标绝对值越大，曲线弧度越大，根据这些规律，完全可以得出一个公式。同时动效老师妥协了一步，将三次贝塞尔曲线改成了二次贝塞尔曲线（只需要一个控制点）。

由我提出控制点的计算公式，进过动效老师的确认，示意图如下。 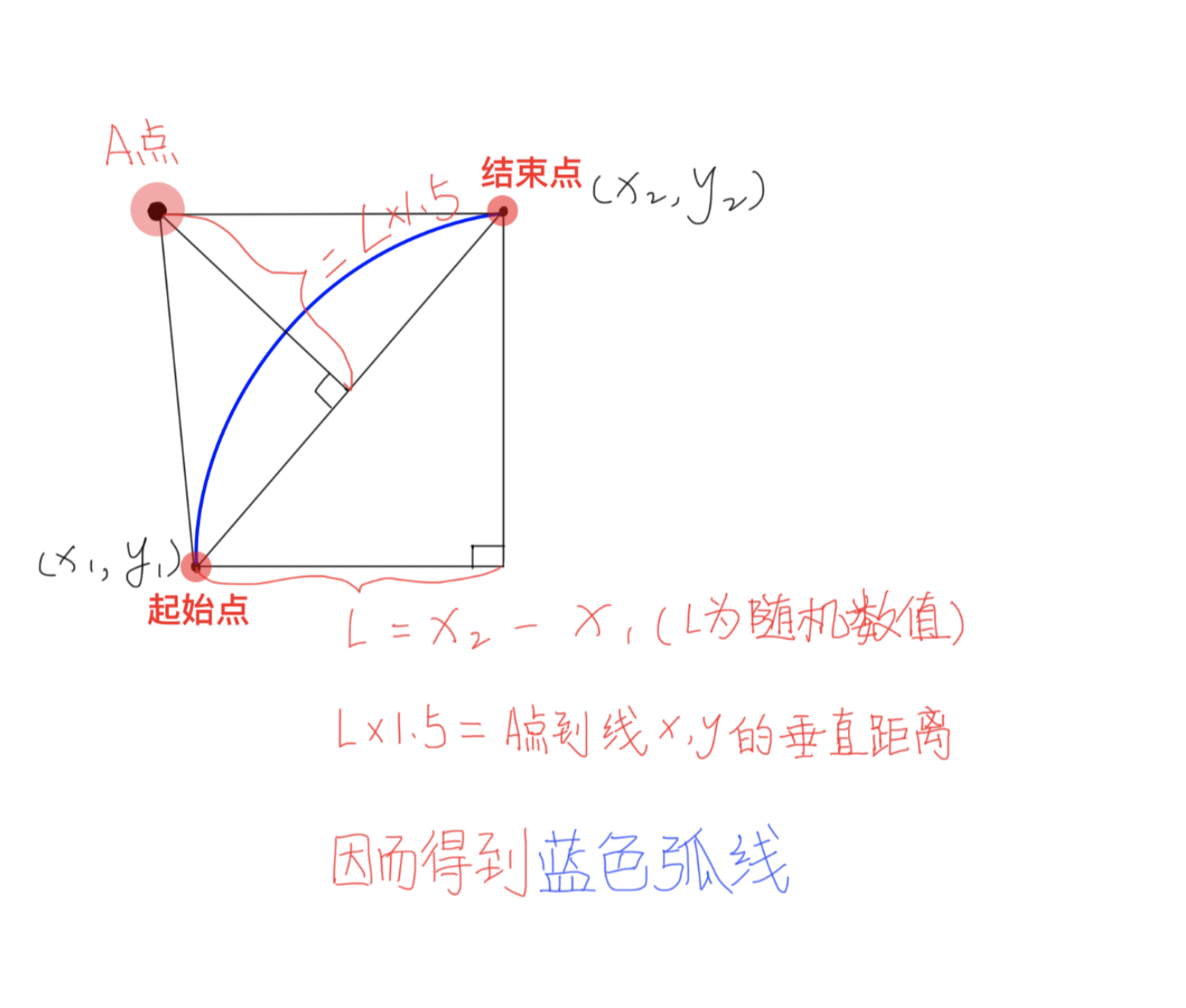接下来就是列公式求坐标了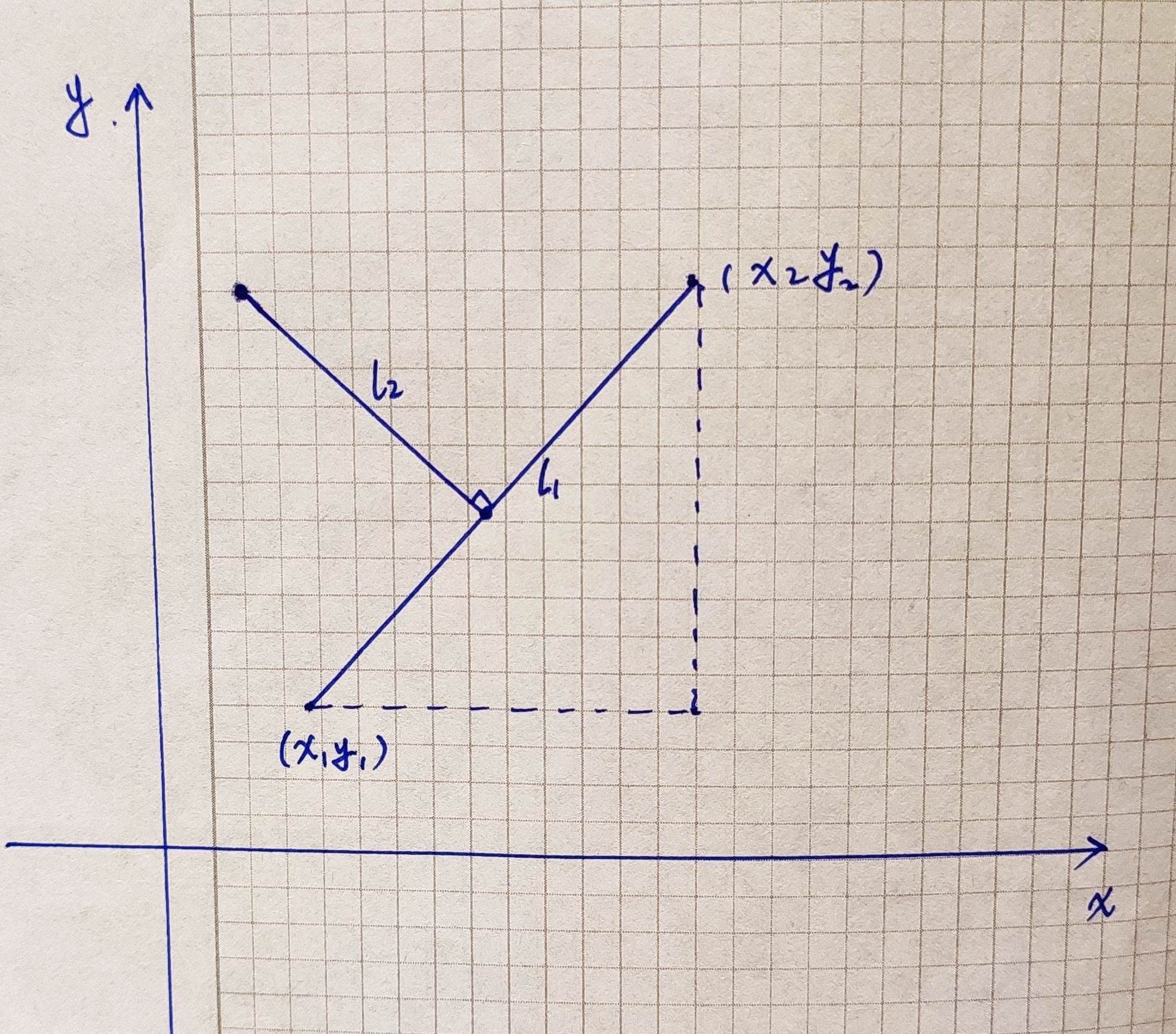！ 起始两点连线的中点坐标可以计算出来，还能计算出 L1 斜率，相差 90 度就是 L2 的斜率。那么，知道直线上一点坐标和直线的斜率，理论上可以计算出直线的解析方程，又知道在这个直线上一点计算另一个距离该点一定距离点的坐标······好麻烦！不会算 😂😂😂，要不要求助一下初中的数学老师 🤔？为了维护大学生的尊严，我又换了一种思路。

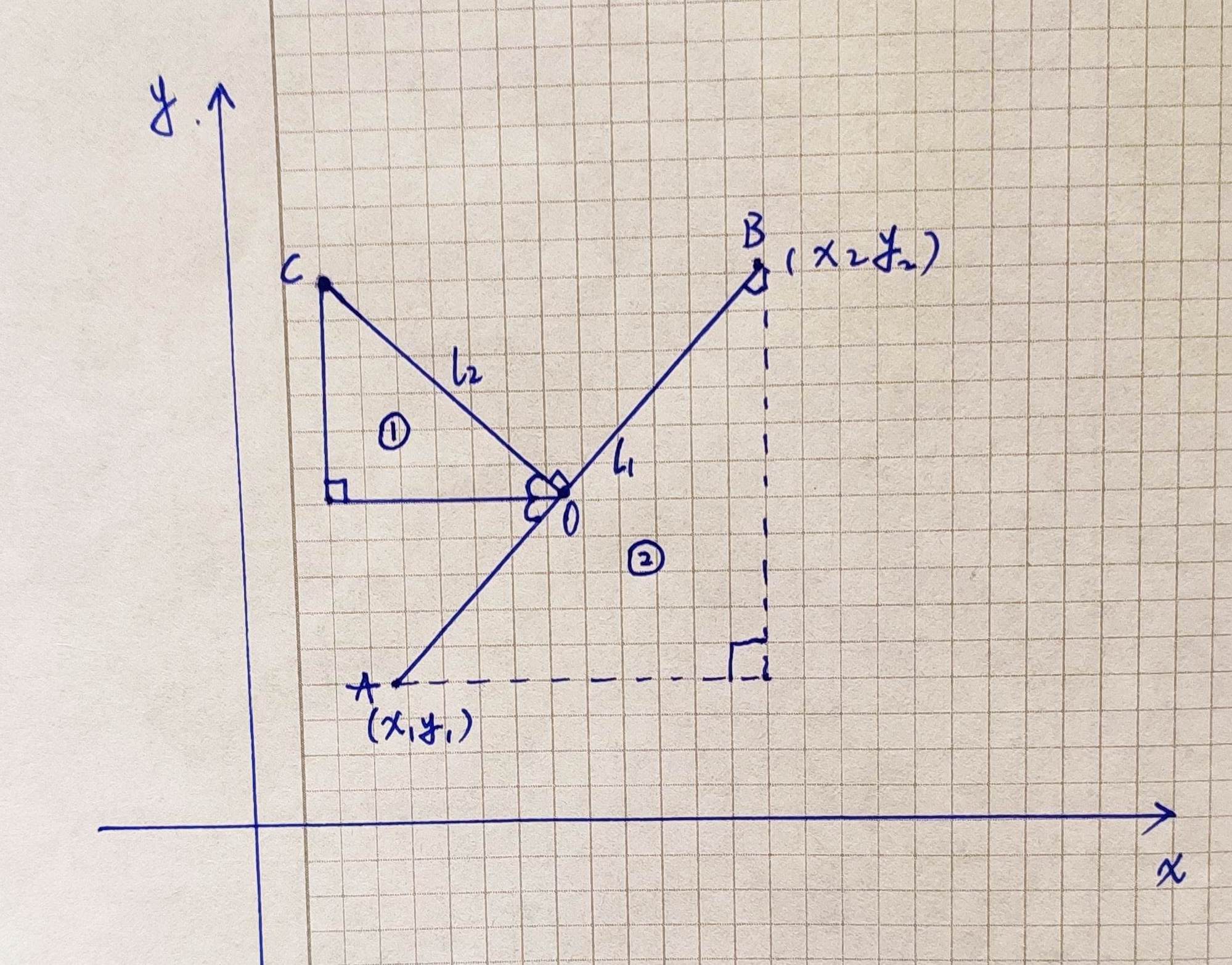大家都知道，三角形 1 和三角形 2 是相似三角形（不知道为什么的同学，主动去问初中数学老师），根据相似三角形理论写出代码：

function getControl(from, to) {
  const x1 = from.x;
  const y1 = from.y;
  const x2 = to.x;
  const y2 = to.y;
  const l = Math.abs(x1 - x2) * 1.5; // 横坐标的差绝对值, 1.5是偏移系数,约大曲线弧度越大
  const L = Math.sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)); // 起始点与终点的直线距离
  const a = (Math.abs(x1 - x2) * l) / L; // 根据相似三角形计算出来的中间变量
  const b = (Math.abs(y1 - y2) * l) / L; // 根据相似三角形计算出来的中间变量
  const midx = (x1 + x2) / 2; // 中点横坐标
  const midy = (y1 + y2) / 2; // 中点纵坐标
  let control; // 二次贝塞尔曲线控制点
  if (x2 > x1) {
    // 如果起点做终点右测,则曲线向左斜
    control = { x: midx - b, y: midy + a };
  } else {
    // 如果起点做终点左测,则曲线向右斜
    control = { x: midx + b, y: midy + a };
  }
  return control;
}

计算出了控制点就可以构建 svg 了

const path = `M${from.x} ${from.y} Q ${control.x} ${control.y} ${to.x} ${to.y}`;
const pathEl = document.createElementNS("http://www.w3.org/2000/svg", "path");
pathEl.setAttribute("d", path);

路径出来，再根据动效老师给的动画时间 duration，效果就实现了！

仔细看动效设计，元素在移动的过程中，自身的大小和旋转角度都在改变，接下来解决这个问题。

解决元素大小和角度变化的问题

大小是时间的函数，动效老师给了起始的大小 0.4，中间的大小 1，最后的大小 0.3。将变化曲线标识在坐标轴上就是这样。 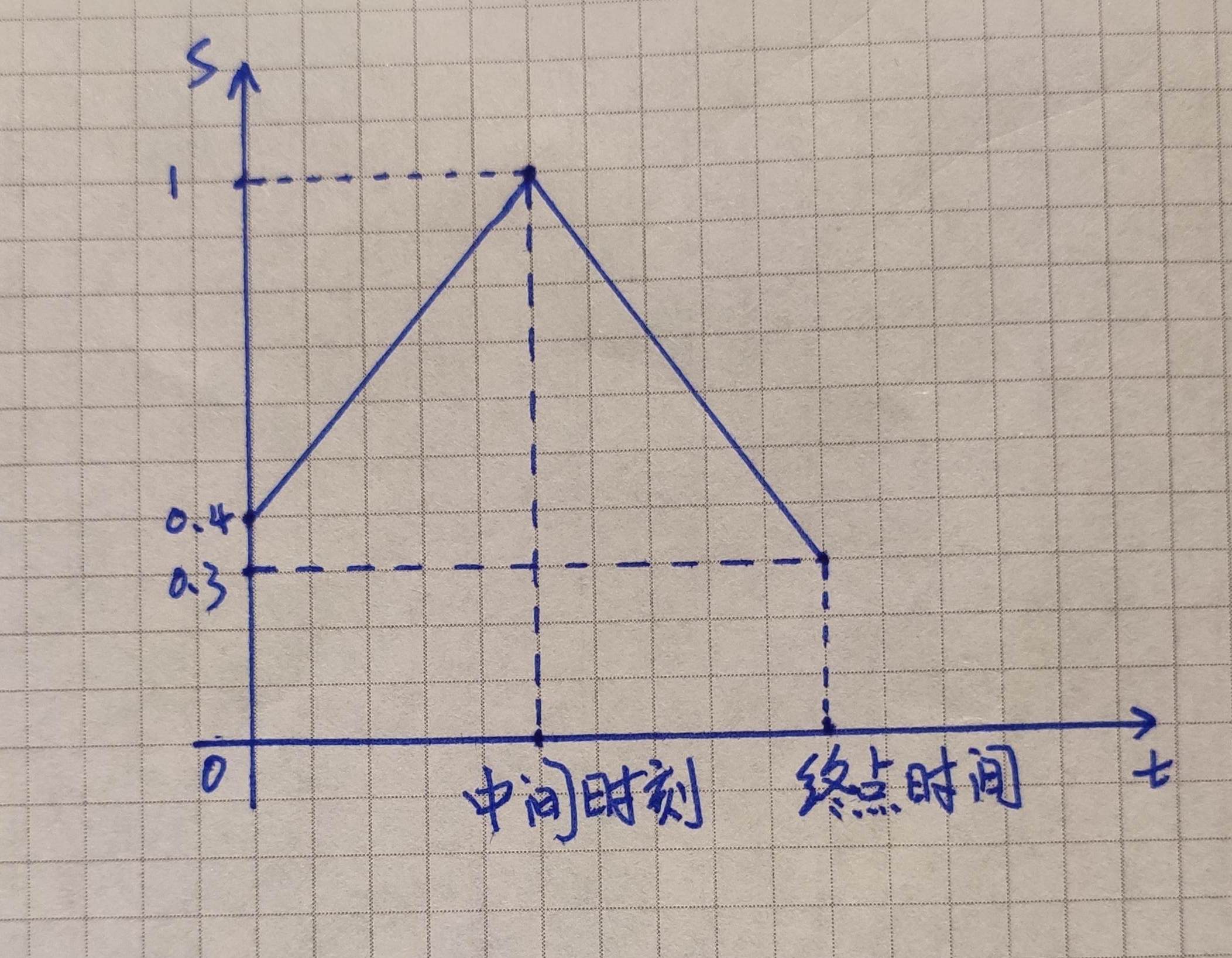变化函数分为两段，每段线段都知道两个端点坐标，数学老师告诉我，这些条件可以求出函数表达式，两段就是两个式子，最后求出是

if (t < 0.5) {
  // 两个坐标点(0,startScale) (0.5,midScale) 求scale对t的函数
  scale = (midScale - startScale) * 2 * t + startScale;
} else {
  // 两个坐标点(0.5,midScale) (1,endScale) 求scale对t的函数
  scale = 2 * (endScale - midScale) * t + 2 * midScale - endScale;
}

将 scale 的变化考虑进去

$e.style.transform = `translate(${curPosition.x}px, ${curPosition.y}px scale(${scale}))`;

剩下的就是旋转角度了，元素的长轴永远是沿着曲线的切线，也就是旋转角度和当时的切线斜率是一致的。如何求曲线的切线？

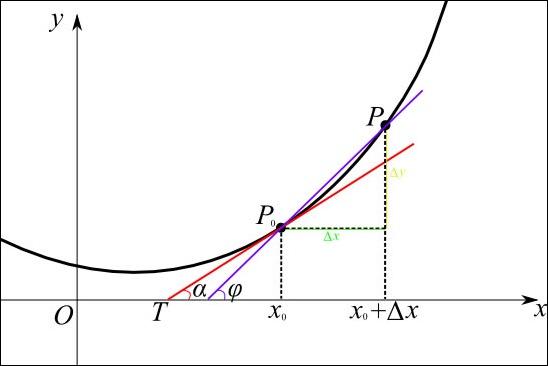几何学上，曲线的割线无限短时，就是曲线的切线。这就将切线问题转化为割线问题，如果我们记录元素移动过程中相邻的两个位置点，根据这两个点求割线的斜率，就接近于真实的切线斜率。

let lastPosition = { x: from.x, y: from.y }; // 记录上一个位置点
function step() {
  ····
  curPosition = pathEl.getPointAtLength(progress); // 当前位置点的坐标
  const rotate = getRotate(lastPosition, curPosition); // 获取当前方向角度
  // 将位置,角度和大小作用到飞点上
  $e.style.transform = `translate(${x}px, ${y}px) rotate(${rotate}deg) scale(${scale})`;
  lastPosition = curPosition;
  ···
}
// 计算切线斜率
function getRotate(lastPos, thisPos) {
  const x1 = lastPos.x;
  const y1 = lastPos.y;
  const x2 = thisPos.x;
  const y2 = thisPos.y;
  const tan_deg = Math.abs(x1 - x2) / Math.abs(y1 - y2);  // 正切值tan/tg
  const deg = Math.atan(tan_deg); // 反函数求角度
  return ((x2 - x1 > 0 ? deg : -deg) * 180) / Math.PI || 0;
}

至此，这次动画效果完整实现了出来。

总结

这次需求涉及到的数学知识很多，如何拟合曲线、路程时间速度计算、相似三角形、求函数表达式（二元一次方程组求解）、求曲线切线斜率。不过还好，都是初高中学到的，还不算超纲。

掌握 SVGPathElement 接口的两个方法 getTotalLength()、getPointAtLength()，能实现无比复杂的移动动画。