业务上遇到了这样的问题, 在浏览器中, 使元素沿着用户画出的路径移动. 因为让元素沿着 svg 路径移动已经实现了, 所以需要做的是用鼠标画出路径. 鼠标方法只能获取鼠标在页面中的实时坐标, 是离散的坐标点, 如何将这些坐标点转化成平滑的路径是问题的关键.
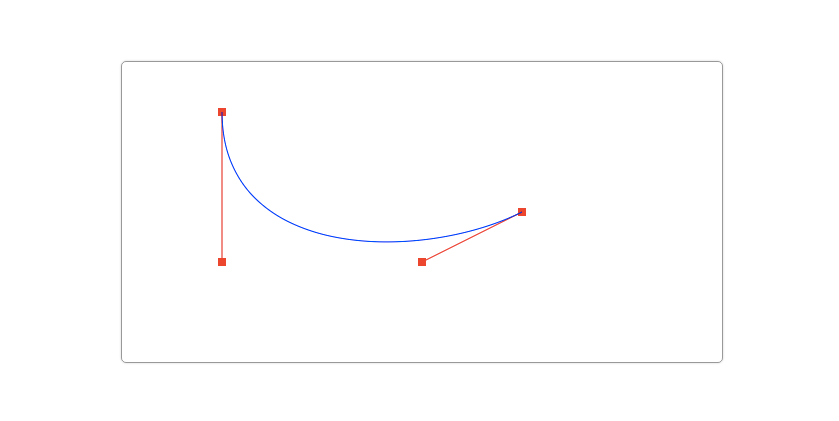svg 的三次贝塞尔曲线需要定义一个点和两个控制点, 所以用 C 命令创建三次贝塞尔曲线, 需要设置三组坐标参数(c dx1 dy1, dx2 dy2, dx dy). 这里的最后一个坐标(dx, dy)表示的是曲线的终点, 另外两个坐标是控制点, (dx1, dy1)是起点的控制点, (dx2, dy2)是终点的控制点. 终点的坐标点好说, 也就是获取的鼠标位置点, 难的是如何得到两个控制点.
网上搜索解决办法, 在百度文库上发现了一篇文章介绍控制点的确定方法(贝塞尔曲线控制点确定的方法). 现在来尝试下用这个方法转化坐标.
假设获取的一系列鼠标坐标保存在数组 data[]中.
const data = [x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6, x7, y7, ...];
以(x3, y3)点为例.
/**
* a为系数，可以尝试不同系数，观察结果
*/
// 后控制点计算
const dx1 = x3 + a(x4 - x2);
const dy1 = y3 + a(y4 - y2);
// 前控制点计算
const dx2 = x4 - a(x5 - x3);
const dy2 = y4 - a(y5 - y3);
那么依次求出每对点的控制点，就能连成一条平滑的曲线了. 开始的一对点作为起点不用求，第二对和最后一对点作为计算点，不做为记录点.
贴上完整代码:
function solve(data, k = 1) {
const size = data.length;
const last = size - 4;
let path = `M${data[0]},${data[1]}`;
for (let i = 0; i < size - 2; i += 2) {
const x0 = i ? data[i - 2] : data[0];
const y0 = i ? data[i - 1] : data[1];
const x1 = data[i + 0];
const y1 = data[i + 1];
// x2 和 y2 作为终点坐标
const x2 = data[i + 2];
const y2 = data[i + 3];
const x3 = i !== last ? data[i + 4] : x2;
const y3 = i !== last ? data[i + 5] : y2;
// 计算控制点
const cp1x = x1 + ((x2 - x0) / 6) * k;
const cp1y = y1 + ((y2 - y0) / 6) * k;
const cp2x = x2 - ((x3 - x1) / 6) * k;
const cp2y = y2 - ((y3 - y1) / 6) * k;
path += ` C${cp1x},${cp1y},${cp2x},${cp2y},${x2},${y2}`;
}
return path;
}