霍夫曼编码(Huffman coding)简介
霍夫曼编码(Huffman Coding),又译为哈夫曼编码、赫夫曼编码,是一种用于无损数据压缩的熵编码(权编码)算法。由美国计算机科学家大卫·霍夫曼(David Albert Huffman)在 1952 年发明。
特点:在计算机资料处理中,霍夫曼编码使用变长编码表对源符号(如文件中的一个字母)进行编码,其中变长编码表是通过一种评估来源符号出现概率的方法得到的,出现概率高的字母使用较短的编码,反之出现概率低的则使用较长的编码,这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。
例如,在英文中,e 的出现概率最高,而 z 的出现概率则最低。当利用霍夫曼编码对一篇英文进行压缩时,e 极有可能用一个比特来表示,而 z 则可能花去 25 个比特(不是 26)。用普通的表示方法时,每个英文字母均占用一个字节,即 8 个比特。二者相比,e 使用了一般编码的 1/8 的长度,z 则使用了 3 倍多。倘若我们能实现对于英文中各个字母出现概率的较准确的估算,就可以大幅度提高无损压缩的比例。
霍夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为 0 层,叶结点到根结点的路径长度为叶结点的层数)。树的路径长度是从树根到每一结点的路径长度之和,记为 WPL=(W1L1+W2L2+W3L3+...+WnLn),N 个权值 Wi(i=1,2,...n)构成一棵有 N 个叶结点的二叉树,相应的叶结点的路径长度为 Li(i=1,2,...n)。可以证明霍夫曼树的 WPL 是最小的。
编码过程
霍夫曼树常处理符号编写工作。根据整组资料中符号出现的频率高低,决定如何给符号编码。如果符号出现的频率越高,则给符号的码越短,相反符号的号码越长。
示例
假设我们要给一个英文单字"F O R G E T"进行霍夫曼编码,而每个英文字母出现的频率如下图。

先创建一个霍夫曼树。
- 将每个英文字母依照出现频率由小排到大,最小在左。
- 每个字母都代表一个终端节点(叶节点),比较 F.O.R.G.E.T 六个字母中每个字母的出现频率,将最小的两个字母频率相加合成一个新的节点。发现 F 与 O 的频率最小,故相加 2+3=5。
- 比较 5.R.G.E.T,发现 R 与 G 的频率最小,故相加 4+4=8。
- 比较 5.8.E.T,发现 5 与 E 的频率最小,故相加 5+5=10。
- 比较 8.10.T,发现 8 与 T 的频率最小,故相加 8+7=15。
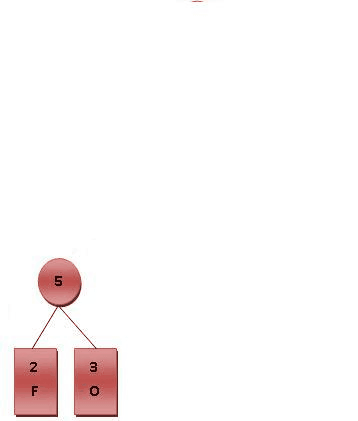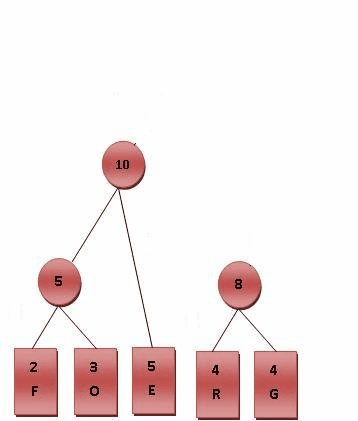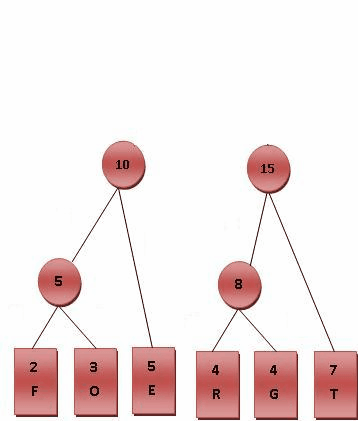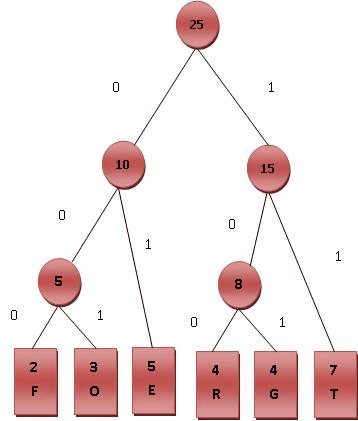
- 最后剩 10.15,没有可以比较的对象,相加 10+15=25。
最后产生的树状图就是霍夫曼树。
进行编码
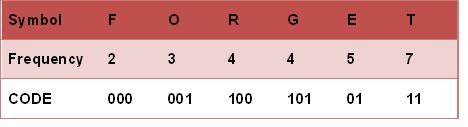
- 给霍夫曼树的所有左链接'0'与右链接'1'。
- 从树根至树叶依序记录所有字母的编码。
https://zh.wikipedia.org/wiki/%E9%9C%8D%E5%A4%AB%E6%9B%BC%E7%BC%96%E7%A0%81